The concept of transport geodesics was introduced in [1] and [4].
They are traces of individual masses that move along a sequence of optimal transport plans.
All such traces turn out to be geodesics under the assumption that the concatenation of those transport plans is also optimal
(i.e., triangle inequality for L1-Wasserstein metric holds with equality).
In short, transport geodesics are shortest paths which are constructed from optimal transport plans.
Here I draw transport geodesics on certain graphs. Masses are transported through a sequence of probability measures 1v0,
μv0, μv1, …, μvn, 1vn,
where v0,v1,…,vn is a diametral geodesic, and 1v is the dirac measure on v, and μv is uniformly distributed measure on the ball of radius 1 around v.
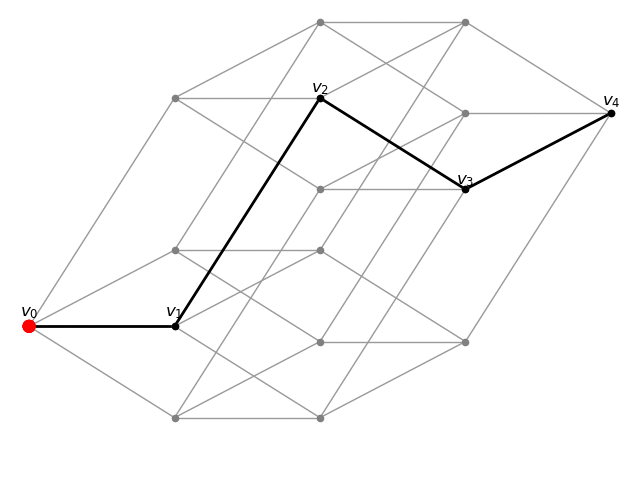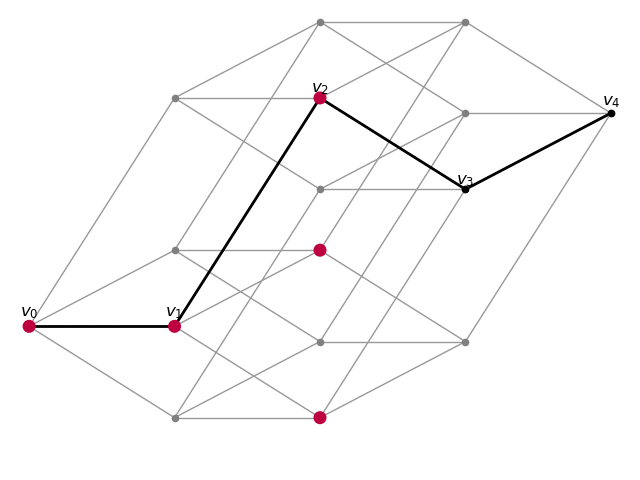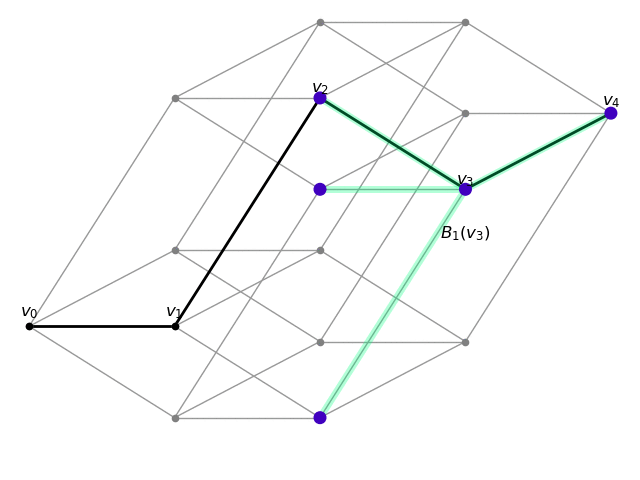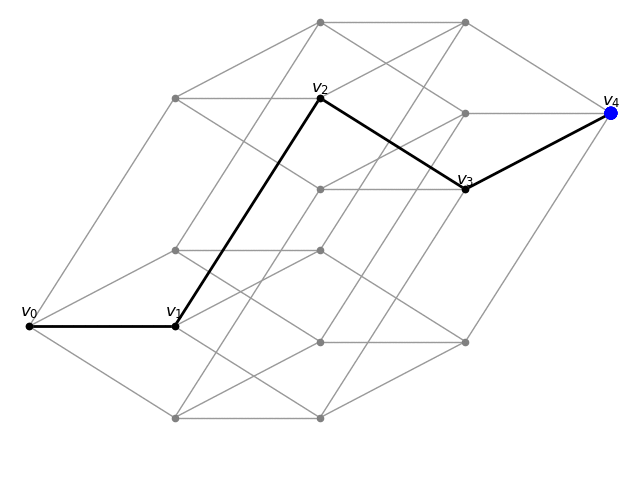4-dimensional cube
Johnson graph J(8,4)
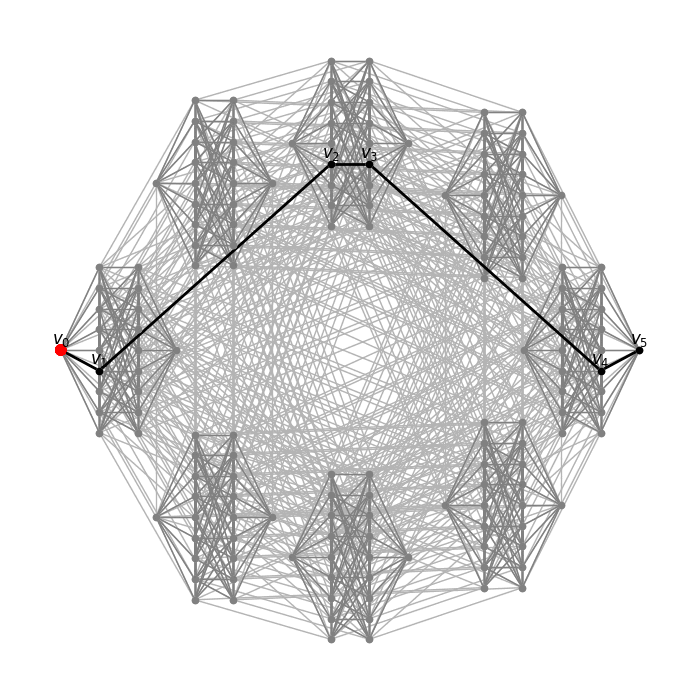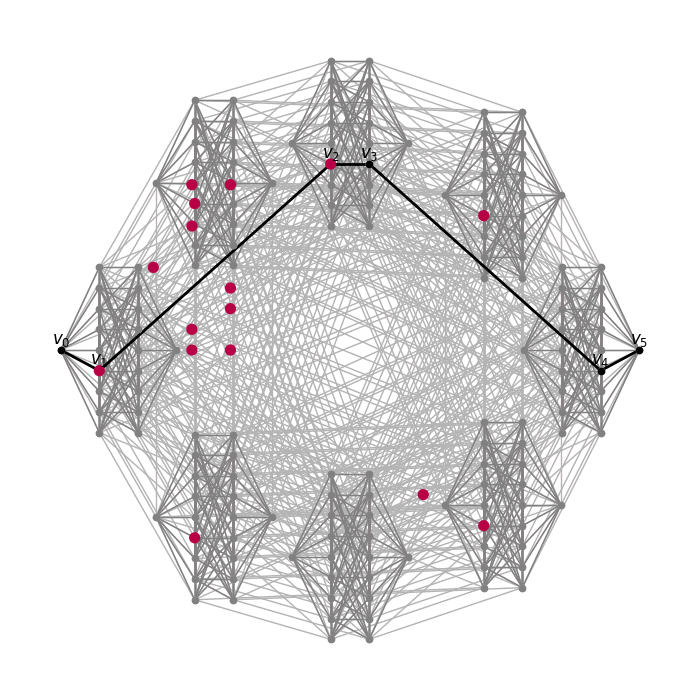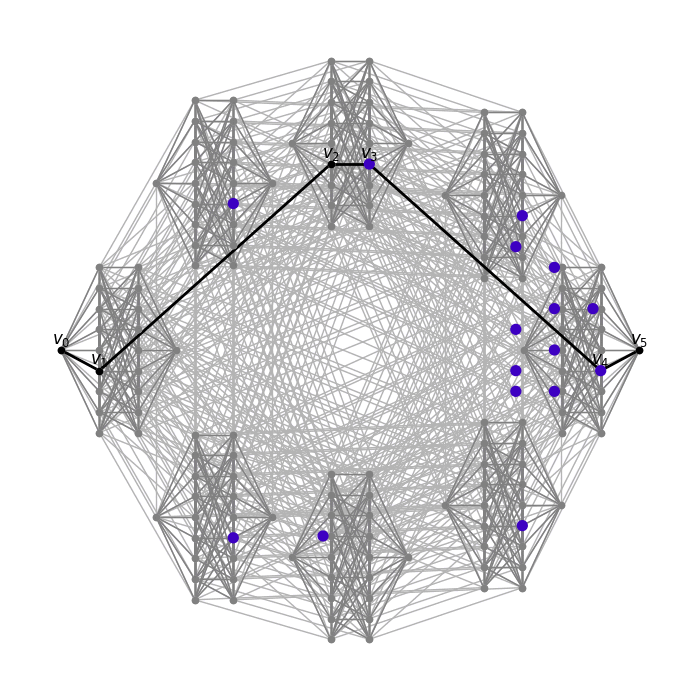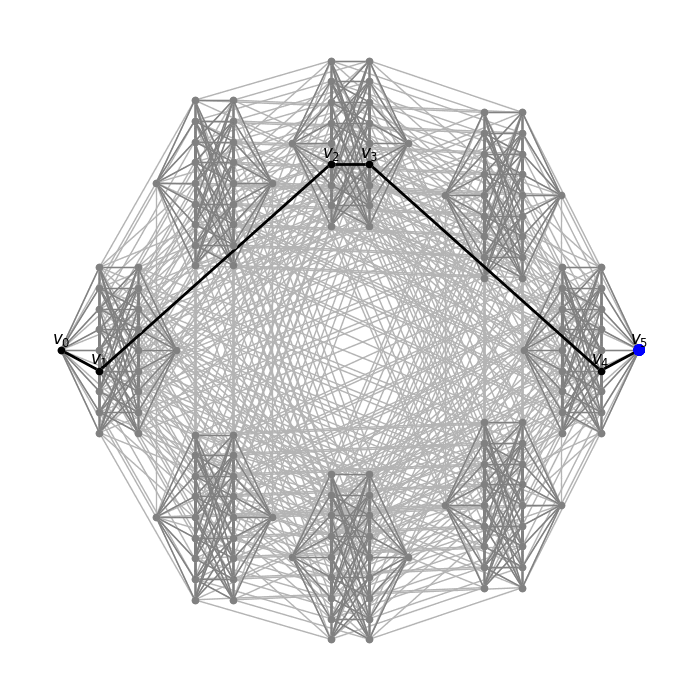Product of cocktail party graph CP(4) and Johnson graph J(6,3)